Probabilidad condicional de falla vs. rata de riesgo |

John Moubray, a manera de advertencia acostumbraba a relatar la siguiente historia a sus aspirantes a consultores RCM:

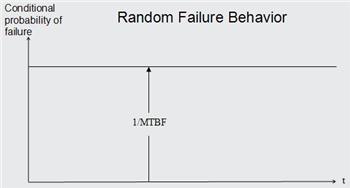
Un consultor profesional RCM recién entrenado estaba dictando el curso estándar RCM de tres días a un grupo de sus clientes. Cuando surgió el tema de falla aleatoria el consultor dibujó el siguiente gráfico en el tablero.

Figura 1 Probabilidad Condicional de falla vs Función de rata de riesgo

Uno de los estudiantes comentó que el gráfico estaba equivocado. El estudiante en desacuerdo manifestó que la probabilidad condicional de falla no era exactamente igual al inverso del tiempo medio entre fallas. El consultor se mantuvo en su posición. Se produjo una acalorada discusión que casi termina en golpes. La amargura perduro el tiempo restante del curso.

Moubray dijo que el estudiante estaba en lo correcto y que el consultor estaba equivocado. Además agregó que el gráfico deja de ser verdadero si el MTTF es inferior a cuatro unidades arbitrarias de tiempo.

¿Cuál es la explicación para esto? ¿No es la probabilidad condicional de falla exactamente igual al inverso del MTTF para un ítem que falla de manera aleatoria? El consultor había sido víctima de la común confusión entre la función de Rata de Falla (también llamada “Rata de riesgo” o “Función de riesgo”) y la Probabilidad Condicional de falla. Los profesionales de RCM y los ingenieros de mantenimiento tienden a pensar en términos de este último, mientras que los matemáticos y los estadísticos utilizan el primero en sus trabajos teóricos. El consultor se pudo haber mantenido en terreno seguro si hubiese denominado el eje vertical “h(t)” o “riesgo” o “rata de falla”. A continuación, la explicación de la declaración de Moubray.

El costado izquierdo de la siguiente ecuación es la definición de la probabilidad condicional de falla.

$P\left(t\leq X\leq t+\Delta t|X\geq t\right)=P\left(0\leq X\leq \Delta t\right)$ (Eqn. 1)

Donde X = el tiempo de falla.

No se deje intimidar por los símbolos matemáticos de la Ecuación 1. La ecuación simplemente muestra en términos matemáticos que la probabilidad condicional de falla en cualquier intervalo Δt es igual a la probabilidad de un ítem nuevo de fallar antes del tiempo Δt. Este podría ser el caso para una falla aleatoria.

También para falla aleatoria, sabemos (por definición) que la probabilidad (acumulativa) de falla en algún momento antes de Δt es dada por:

$P\left(0\leq X\leq \Delta t\right)=1-e^{-\frac{\Delta t}{MTTF}}$

Ahora dejemos que MTTF = kΔt y dejemos que Δt = 1 unidad arbitraria de tiempo. Entonces, la Probabilidad Condicional de falla es exactamente:

$P\left(0\leq X\leq \Delta t\right)=1-e^{-\frac{1}{k}}$

Escribamos ahora e^x como una serie infinita

$e^{x}=1+x+\frac{x^{2}}{2}+\frac{x^{3}}{6}+\dots$

Entonces, para x = -1/k

$e^{-\frac{1}{k}}=1-\frac{1}{k}+\frac{1}{2}\left(-\frac{1}{k} \right)^{2}+\frac{1}{6}\left(\frac{1}{k} \right)^{3} +\dots$

Re-ordenando, la Probabilidad Condicional es

$1-e^{-\frac{1}{k}}=\frac{1}{k}+\frac{1}{2}\left(-\frac{1}{k} \right)^{2}+\frac{1}{6}\left(\frac{1}{k} \right)^{3} +\dots$ Exactamente, o

$1-e^{-\frac{1}{k}}=\frac{1}{k}$ Aproximadamente.

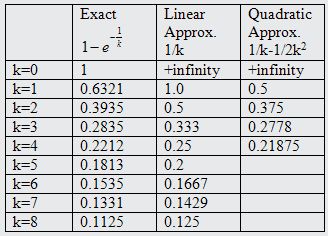
Calculemos los valores exactos y aproximados (usando el primer término y los dos primeros términos de la expansión de la serie infinita para e^x) para la probabilidad condicional de falla en la tabla:

Conociendo que k=MTBF/Δt, podemos ver que si el MTBF es grande en relación con el intervalo de observación Δt, la probabilidad condicional de falla está bien aproximada por el inverso del MTBF.

Observando esta tabla, la aproximación del factor de 4 de Moubray es muy buena.

Articulos similares

Tiempo a la falla (50%)
El Elusivo Intervalo P-F (50%)

Probabilidad condicional de falla vs. rata de riesgo

One Response to Probabilidad condicional de falla vs. rata de riesgo

Buscar

Categorias

Articulos recientes

Forums

Otras Acciones

Regresar a la Página Principal

Contáctenos en: