Conditional probability of failure

The most powerful information sought by all maintenance engineers and managers boils down to the conditional failure probability. It is the probability of an item failing in an upcoming period of interest knowing that it is currently in an unfailed state. If you knew that the conditional probability of failure of a given part or component were unusually high you could channel your manpower to intervene propitiously, thereby preempting the consequences of a failure in service while avoiding waste of resources and unnecessary downtime on items where failure is not imminent.

Other articles^[1] describe how to calculate the conditional probability of failure of an item. In this article we’ll discuss Conditional Probability first and then we’ll define the Conditional Probability of Failure.

Conditional Probability

Let’s begin with a card experiment. A card is chosen at random from a standard deck of 52 playing cards. Without replacing it, a second card is chosen. What is the probability that the first card chosen is a queen and the second card chosen is a jack? The events are said to be dependent because the probability of the second depends on the first.

A. P(queen on first pick) = 4/52
B. P(jack on 2nd pick given queen on 1st pick) = 4/51, a higher probability than 4/52

Then the probability that both events occur P(queen and jack)= (4/52)(4/51)=4/663

The probability of choosing a jack on the second pick given that a queen was chosen on the first pick is called a conditional probability. The conditional probability of an event B in relationship to an event A is the probability that event B occurs given that event A has already occurred. The notation for conditional probability is P(B|A) ^[2].

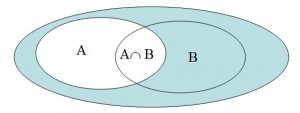
When two events, A and B, are dependent, the probability of both occurring (denoted by “A∩B”) will, according to the card experiment, be the product of their probabilities, that is:

P(A∩B) = P(A) · P(B|A) , or

When two events are dependent (the probability of one depends on the other’s occurrence) their probability areas intersect in a Venne graphical representation.

Conditional Probability of Failure

Suppose the two dependent events were:

1. X>t, an item survives to time t, X being the time of failure, and
2. t≤X≤t+Δt, the item fails in the interval between t and t+Δt given event 1.

As in the card experiment the probability of the second event depends on the first. Then the Conditional Probability of Failure is:

It is the probability of failure in the interval between t and t+Δt (analogous to selecting a jack on the second pick) given that the item has survived to time t (analogous to selecting a queen on the first pick).

The article here shows that the conditional failure probability is a special case of the conditional probability where the numerator reduces simply to P(t≤X≤t+Δt). So that:

© 2014, Murray Wiseman. All rights reserved.

1. ^[1]See for example here and here.↩
2. ^[2]pronounced as “The probability of event B given A”↩